Tools and Guidance for Applying Neural Networks to Eddy Covariance Data

June Skeeter
june.skeeter@ubc.ca

University British Columbia

Eddy Covariance

Semi-continuous, ecosystem-scale energy, water, and trace gas fluxes.

  • Noisy, voluminous data sets
    • Frequent gaps
    • Observational bias
  • Well suited for machine learning!

your-image-description

Burns Bog EC Station
Delta, BC

Neural Networks

Universal approximators: can map any continuous function to an arbitrary degree accuracy.

  • With enough hidden nodes, will fit any pattern in a dataset
    • Care must be taken to ensure the patterns are real
    • Early stopping can help prevent over-fitting
  • Well suited for non-linear, multi-variate response functions
    • Capable of interpolation and extrapolation

Commonly Cited Limitations

Issue Solutions
Over-fitting - Model ensembles
- 3-way cross validation
- Pruning inputs
Black boxes models - Plot partial derivatives
- Feature importance
Computationally expensive - Tensorflow
- GPU processing

Objective

Provide a framework for applying NN models to EC data for descriptive analysis and inferential modelling.

  • The github repository linked here has functional examples that can be used to setup NN models.
    • Runs in Python and Tensorflow
      • GPU support not required
        • But will decrease processing times

Example Data

Burns Bog EC station

  • Harvested peatland undergoing active restoration
  • 8+ years of flux data

your-image-description

Training Procedures

  • Larger ensemble = more robust model
    • N \(\leq\) 10 for data exploration/pruning
  • Three way cross-validation
    • Train/validate/test
  • Early Stopping: after e epochs
    • e = 2 for pruning stage

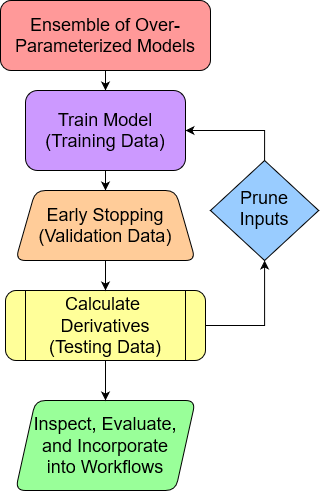
your-image-description

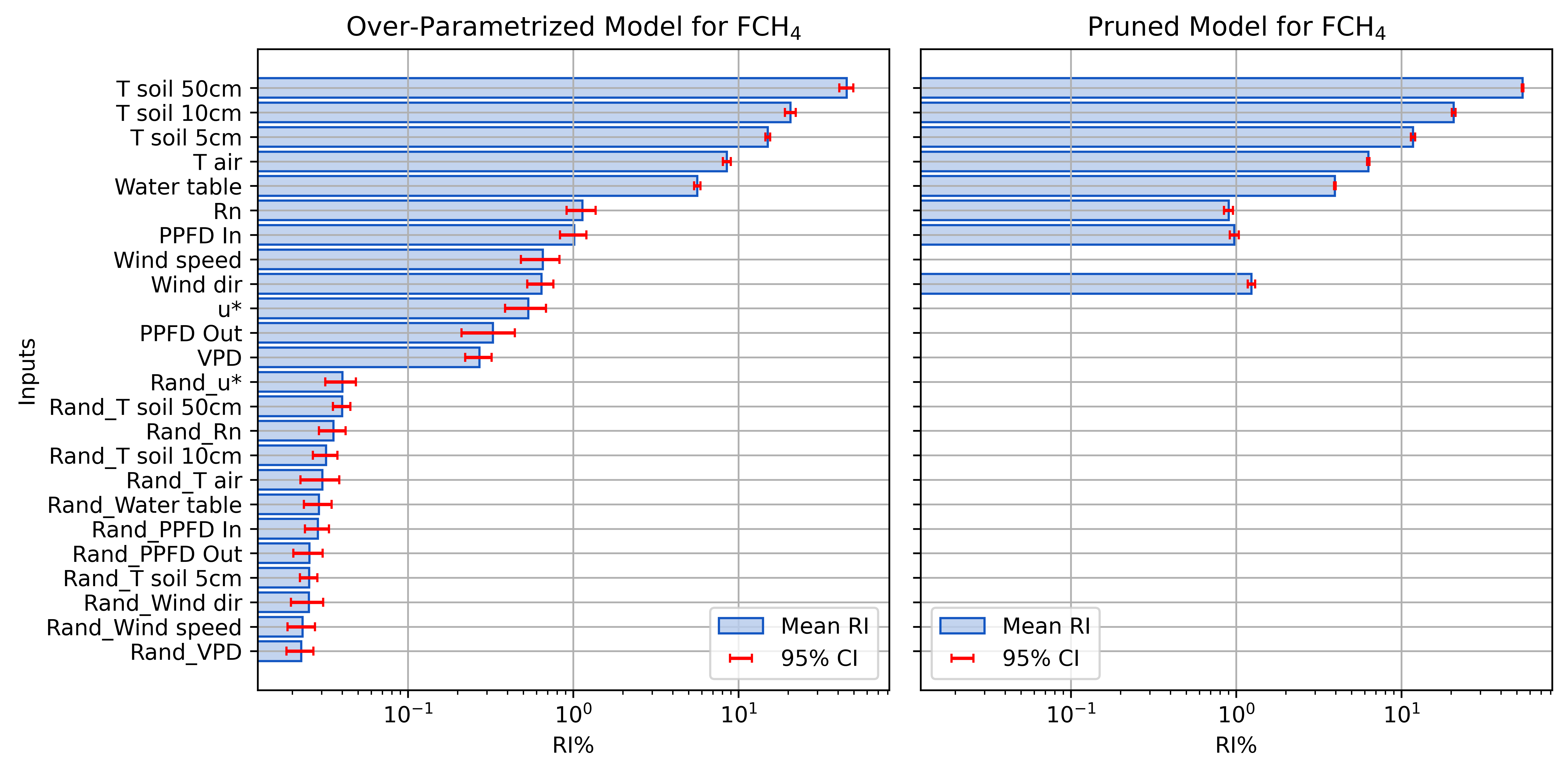
Pruning Inputs

Calculate partial first derivative of the output with respect to each input over test data domain.

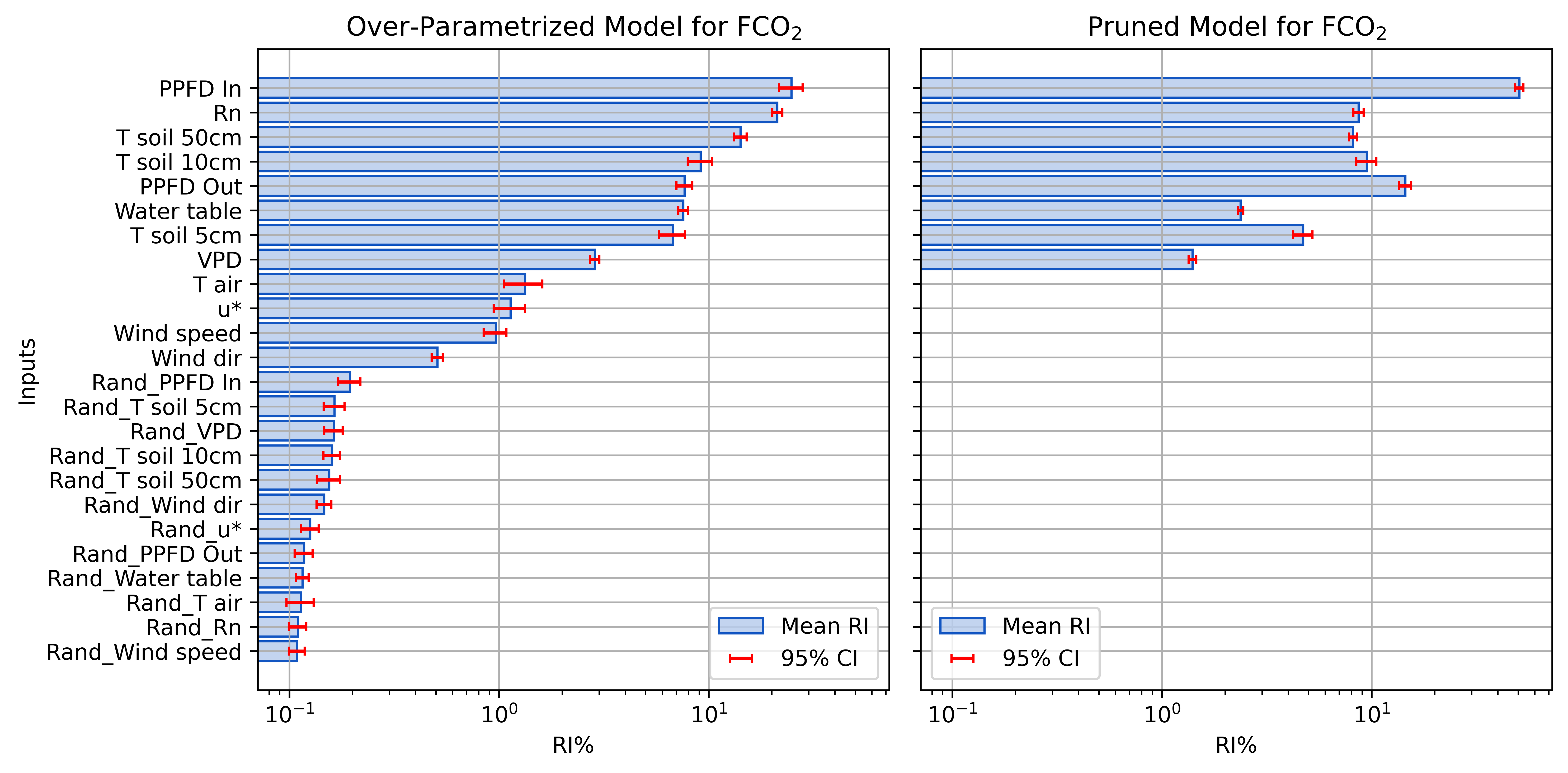
  • Relative Influence (RI) of inputs
    • Normalized sum of squared derivatives (SSD)
  • Iteratively remove inputs with RI below a threshold
    • Use random noise to determine threshold
      • e.g., randomly shuffled copy of each input

Before and After Pruning FCO2

The Final Model

Once pruning is complete, re-train the final production level model, excluding the random scalars

  • Increase the ensemble size (e.g., N \(\geq\) 30)
    • Increase early stopping (e) criteria (e.g., e = 10)
      • Larger e drastically increases training time
  • Plot the model derivatives as a final check
    • If derivatives look implausible
      • Adjust inputs/parameters and try again

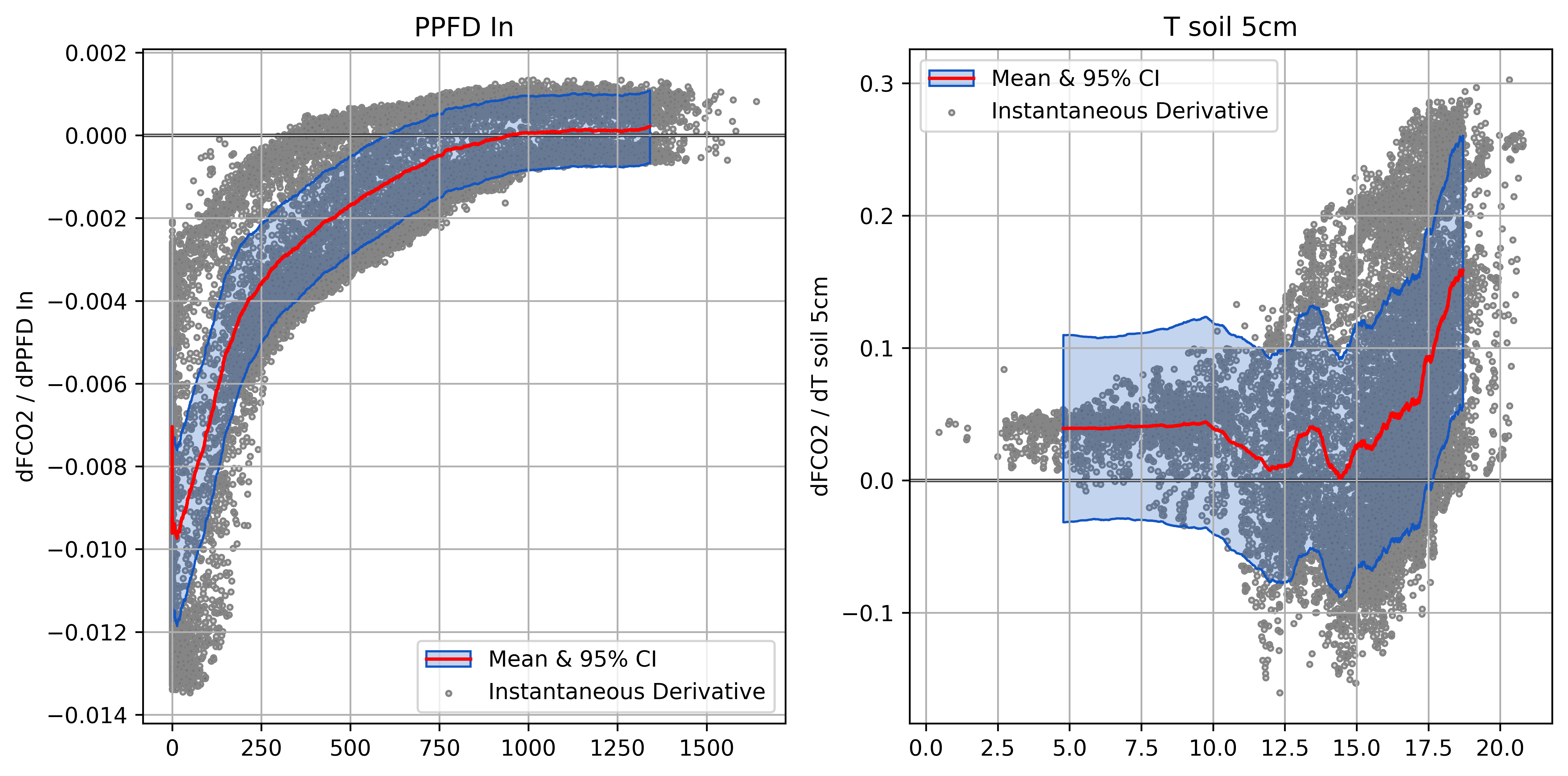
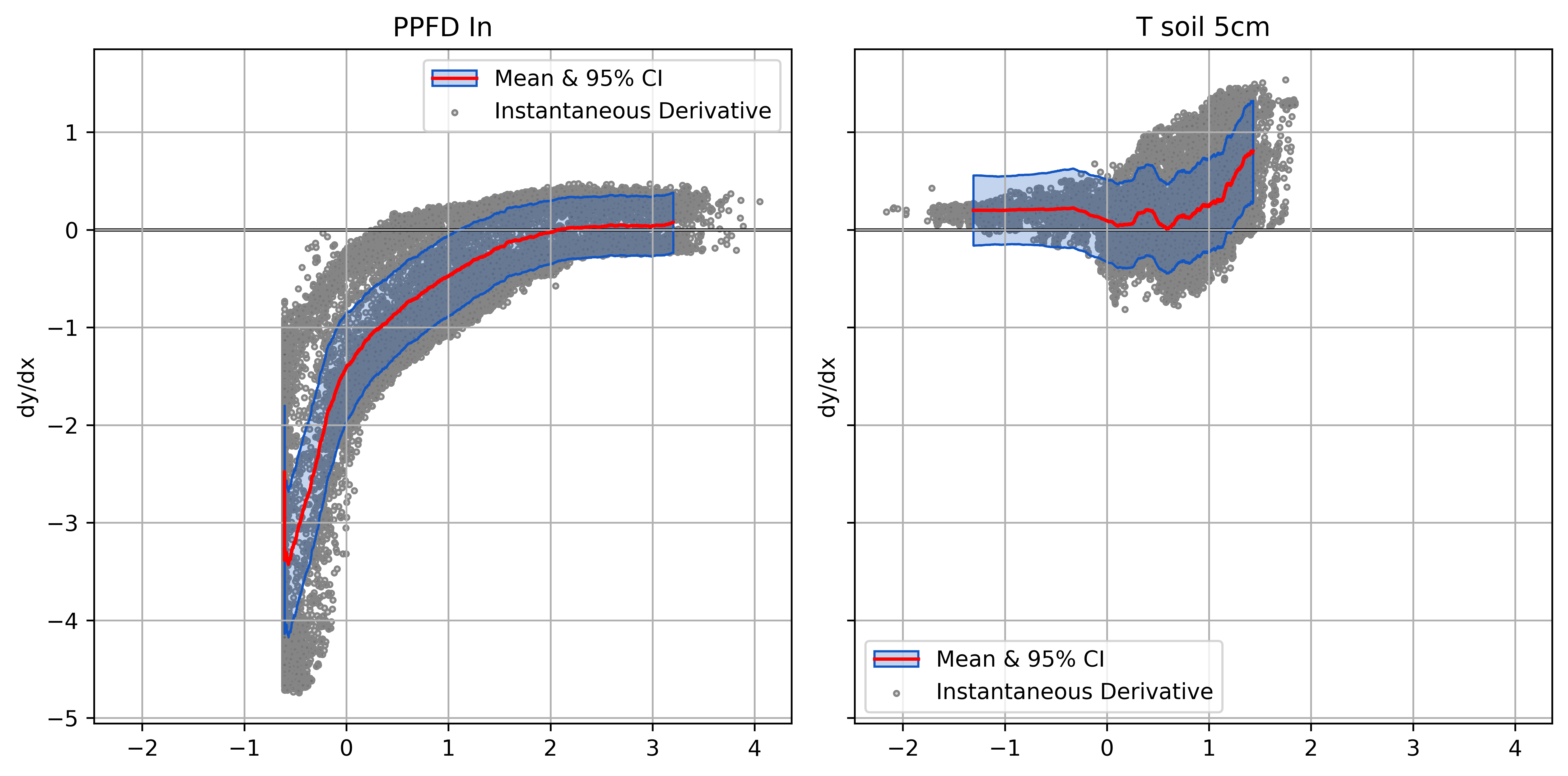
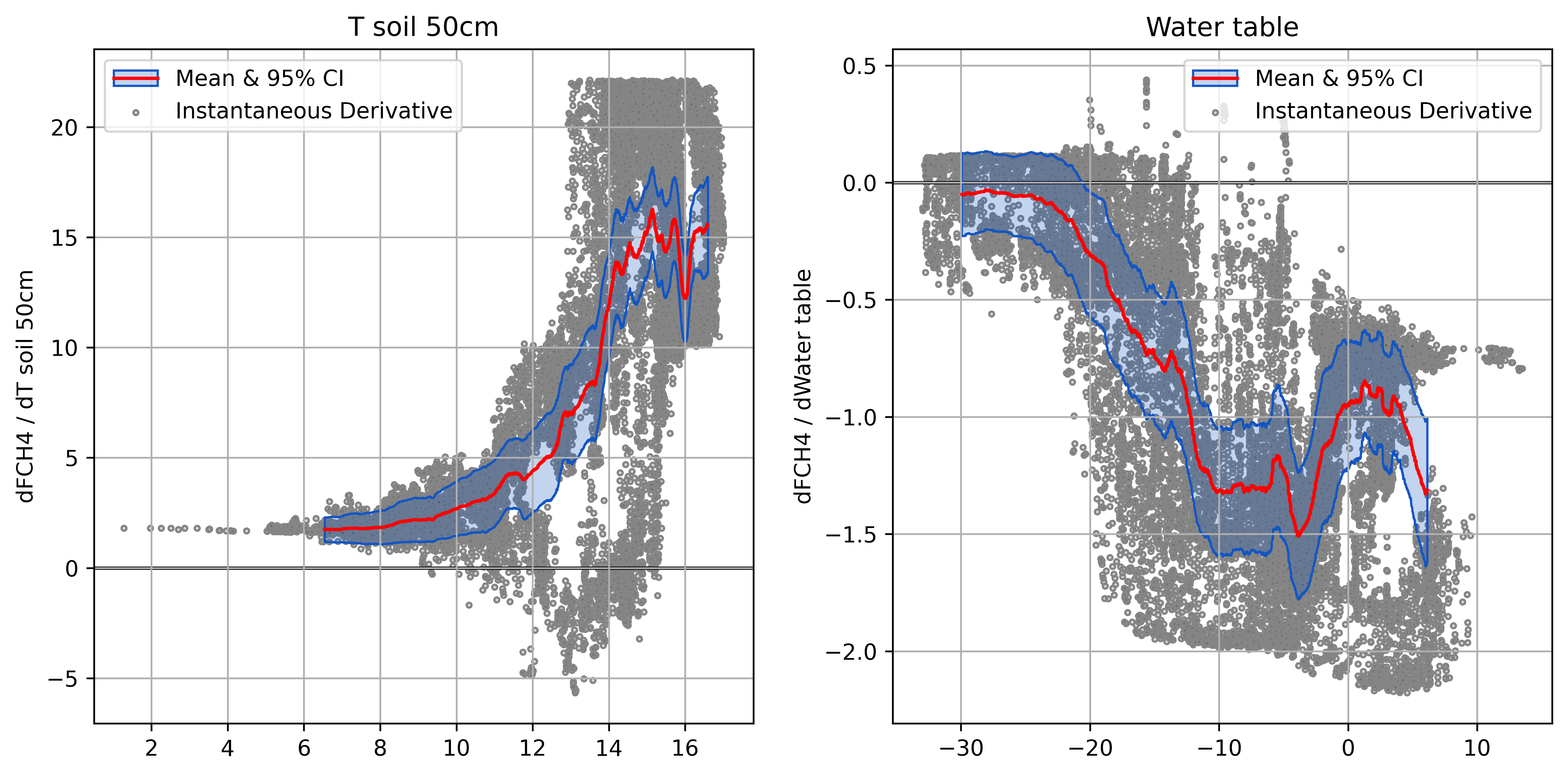
Plotting Derivatives

Helps ensure model responses are physically plausible

  • An essential step and key advantage of NN models
  • Raw derivatives show response in natural units
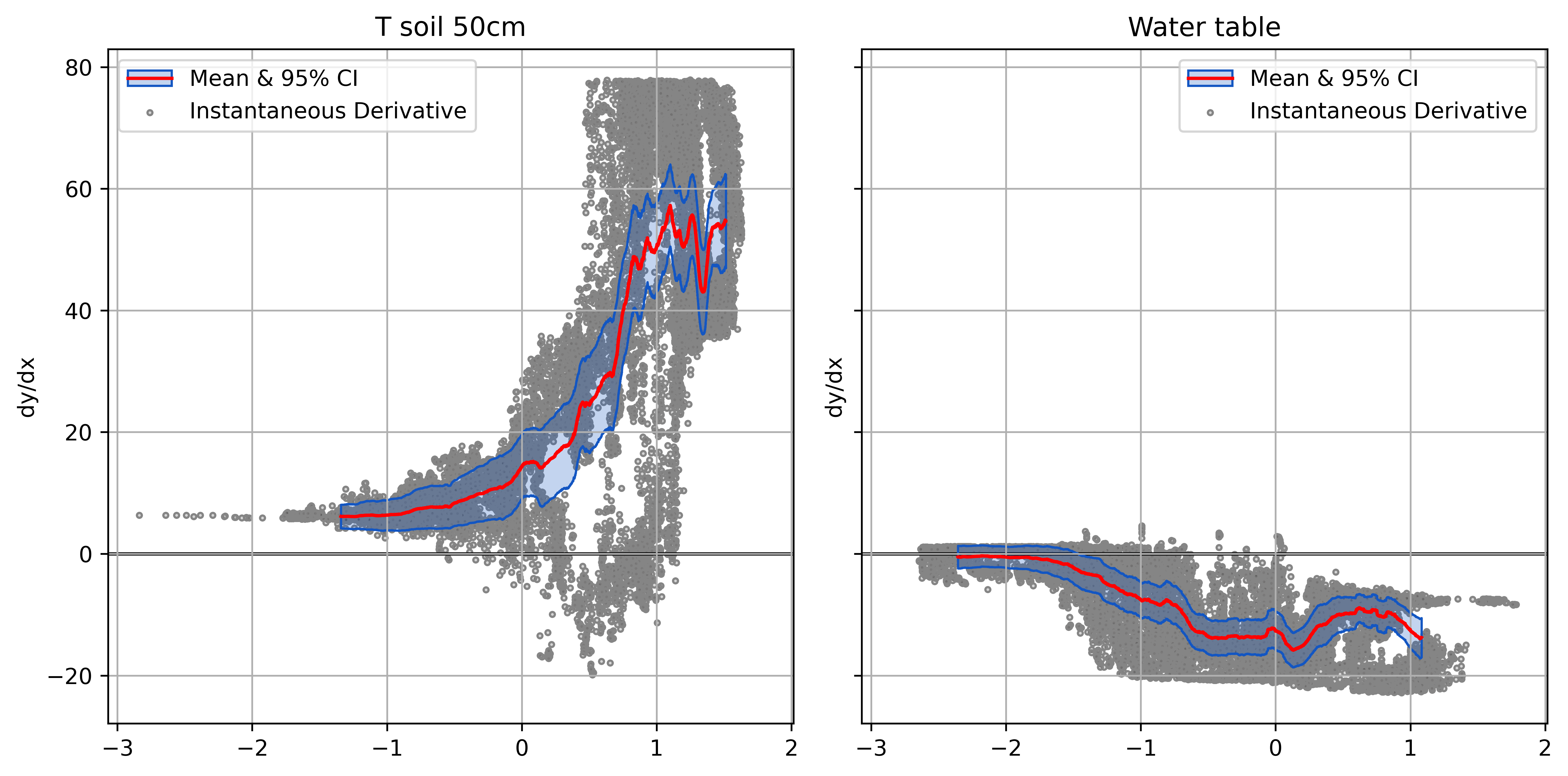
  • Normalized derivatives scaled by input variance
    • Relative input effects on common scale
    • What the model “sees”

Partial Derivatives of FCO2

Normalized Derivatives of FCO2

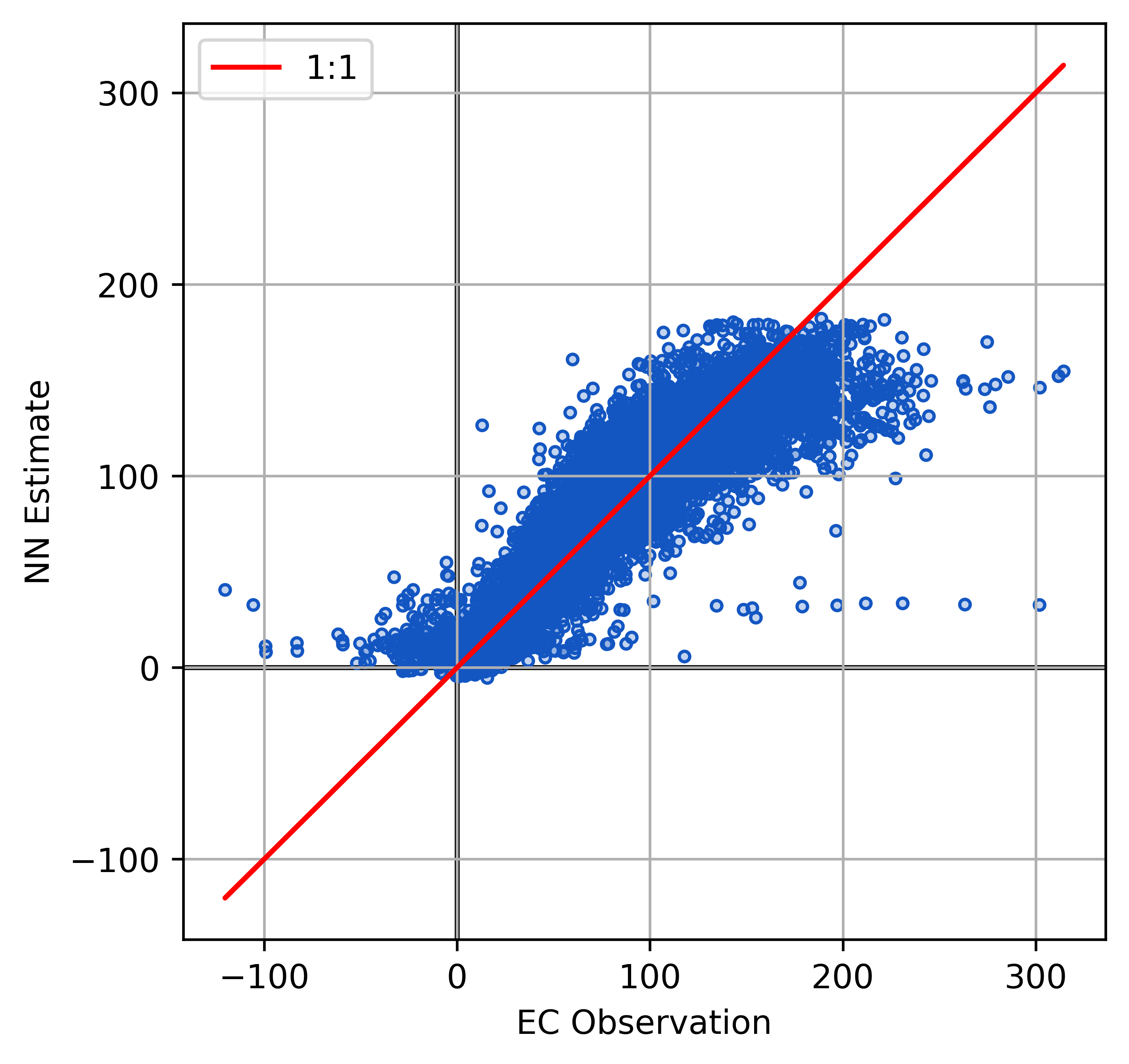
Model Performance FCO2

Plot the model outputs and validation metrics calculated with the test data.

Metric Score
RMSE 0.64 \(\mu mol\) \(m^{-2}s^{-1}\)
r2 0.88

Before and After Pruning FCH4

Partial Derivatives of FCH4

Normalized Derivatives of FCH4

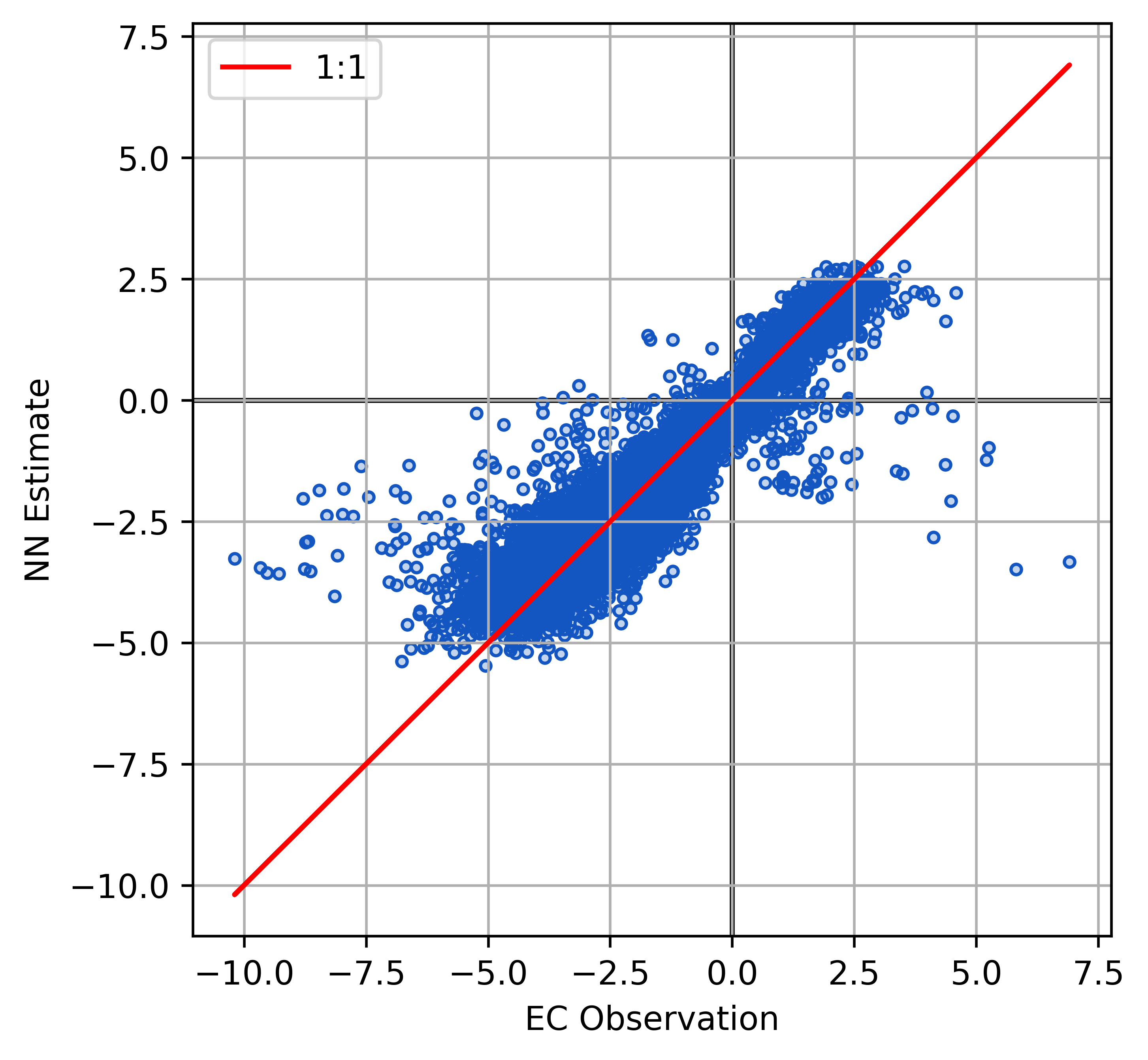
Model Performance FCH4

Plot the model outputs and validation metrics calculated with the test data.

Metric Score
RMSE 17.17 \(nmol\) \(m^{-2}s^{-1}\)
r2 0.89

Next Steps

  • Custom NN architecture: Separating input layers may allow us partition fluxes.
    • e.g., FCO2 into GPP and ER
  • Flux footprints: map response to spatial heterogenity
  • Upscaling: in space and time
  • u* filtering: partial derivatives could identify u* thresholds
  • Compare to process based models (e.g., CLASSIC)

Thank You

Questions?