Projected Coordinate Systems
A map projection is a flattened GCS. Imagine sending rays of light through the ellipsoid onto a flat surface, the resulting image is a projection.
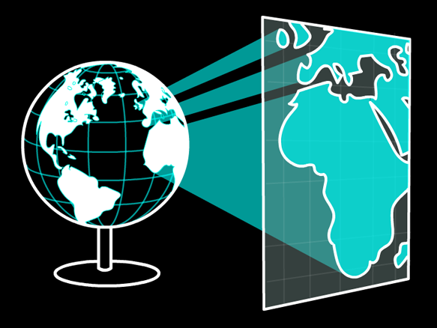
How do we construct projections?
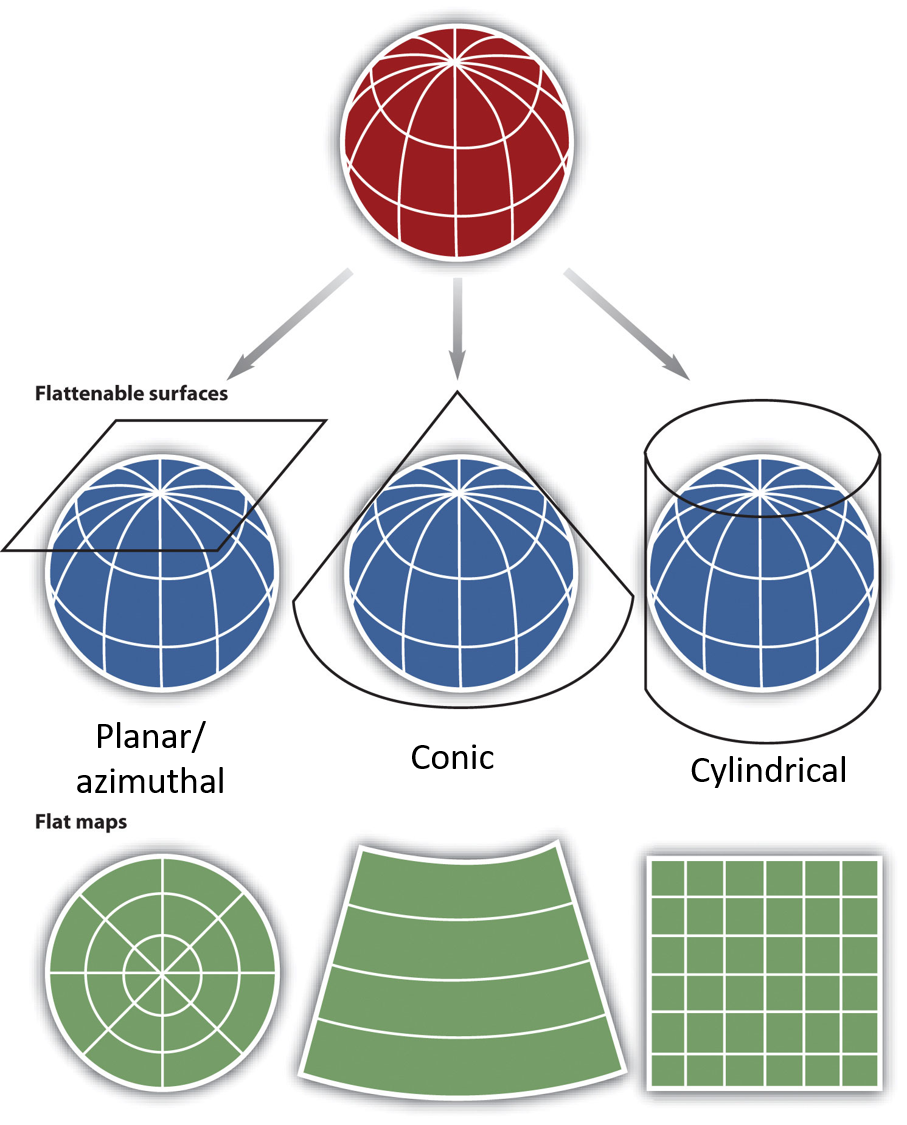
A GCS is projected onto a surface that can be flattened.
Planar: A 2D flat plane
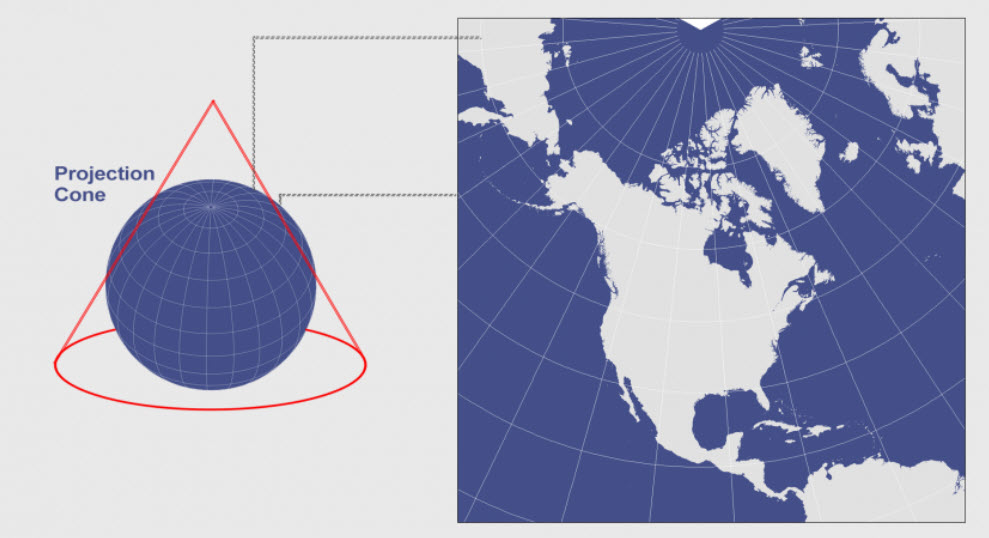
Conic: A 2D cone
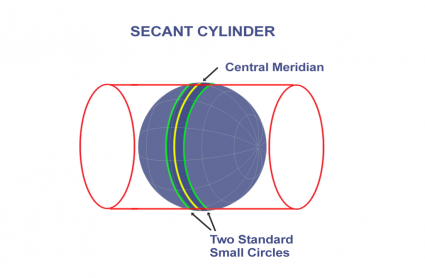
Cylindrical: A 2D cylinder
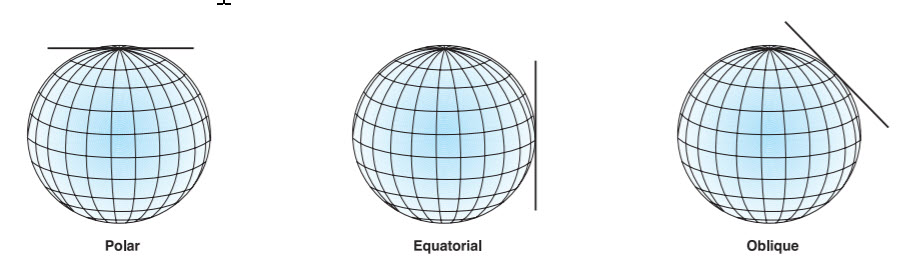
Planar/Azimuthal
Simplest option but limited applicability/scope. Usually only used for polar regions.
Planar/Azimuthal
Planar/Azimuthal
Conic
Great for mid-latitudes. Can only cover one hemisphere at a time.
Conic: BC Albers
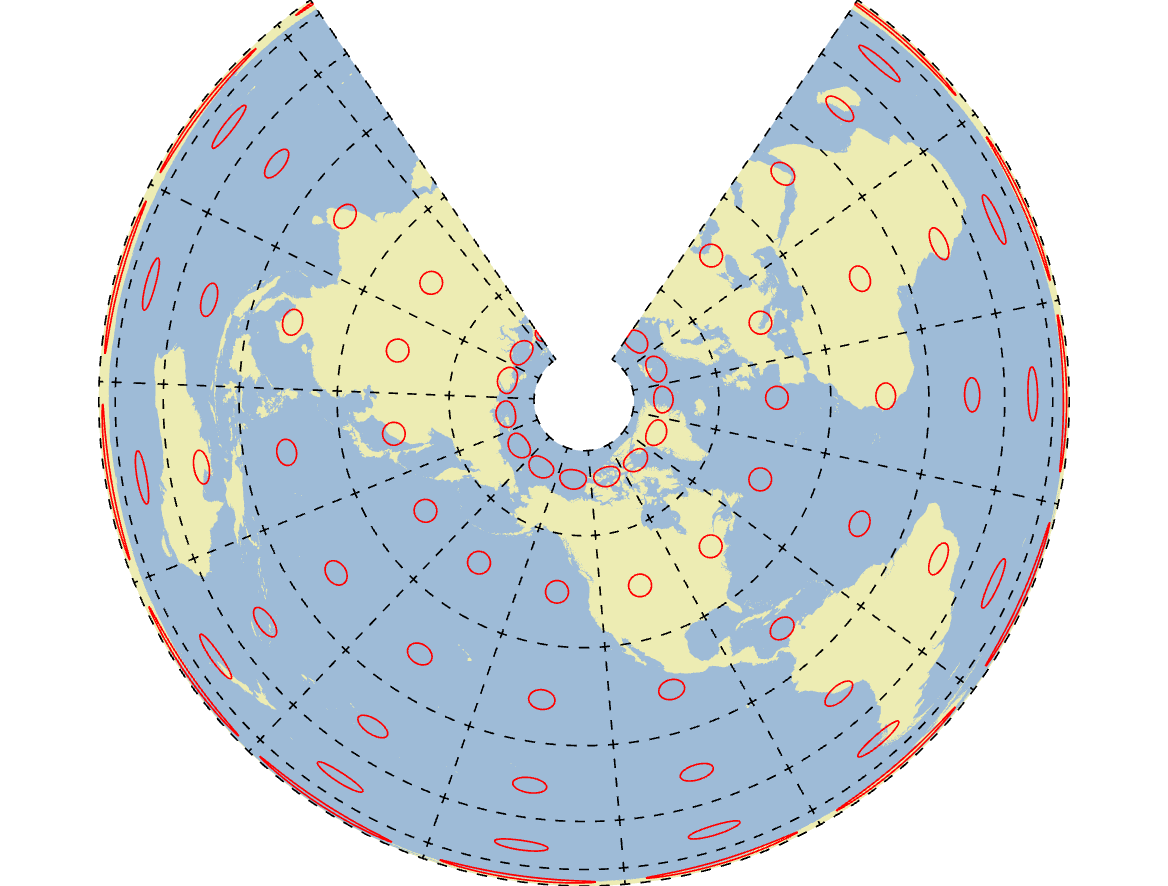
Conic: Canada Lambert
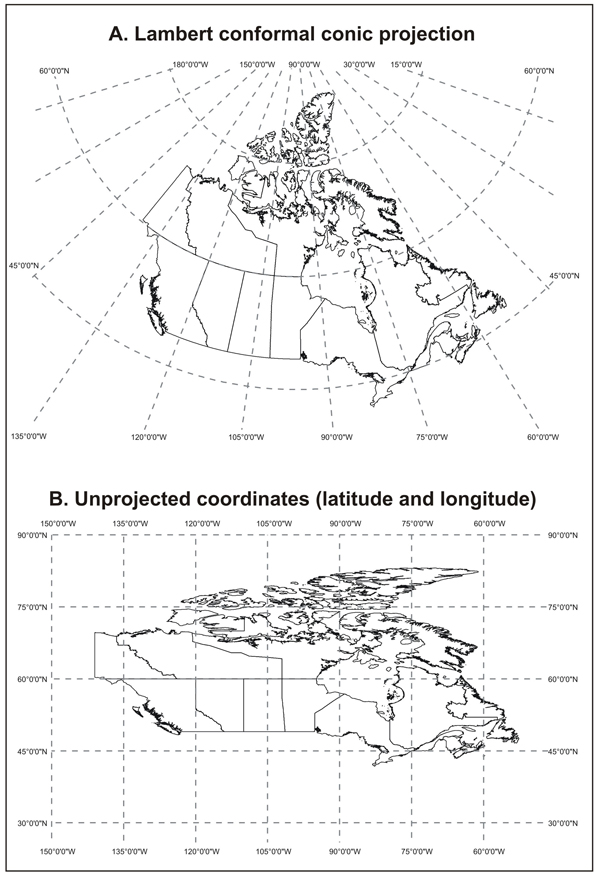
Conic Projection vs. Latitude/Longigude
Conic Projection - Nicely accounts for curvature of the earth.
Lat/Lon - Scruched & distorted image when displayed in 2 dimmensions.
Cylindrical
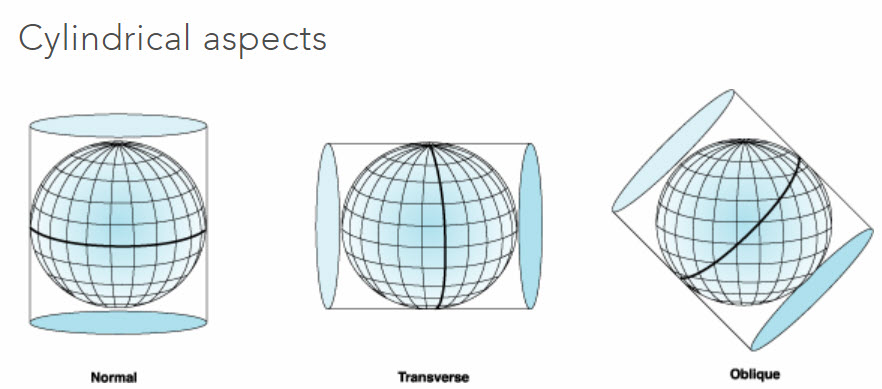
Works for the full Earth (Normal). Or applied to small slices (Transverse)
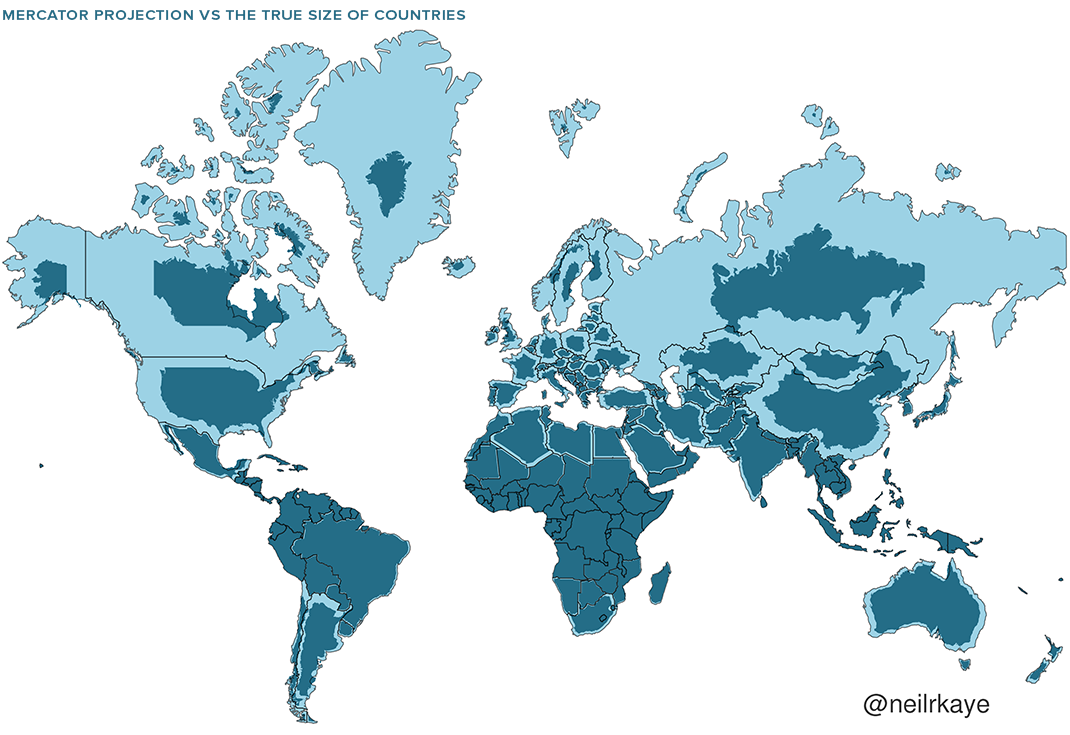
Cylindrical: Mercator

Cylindrical: Sinusoidal
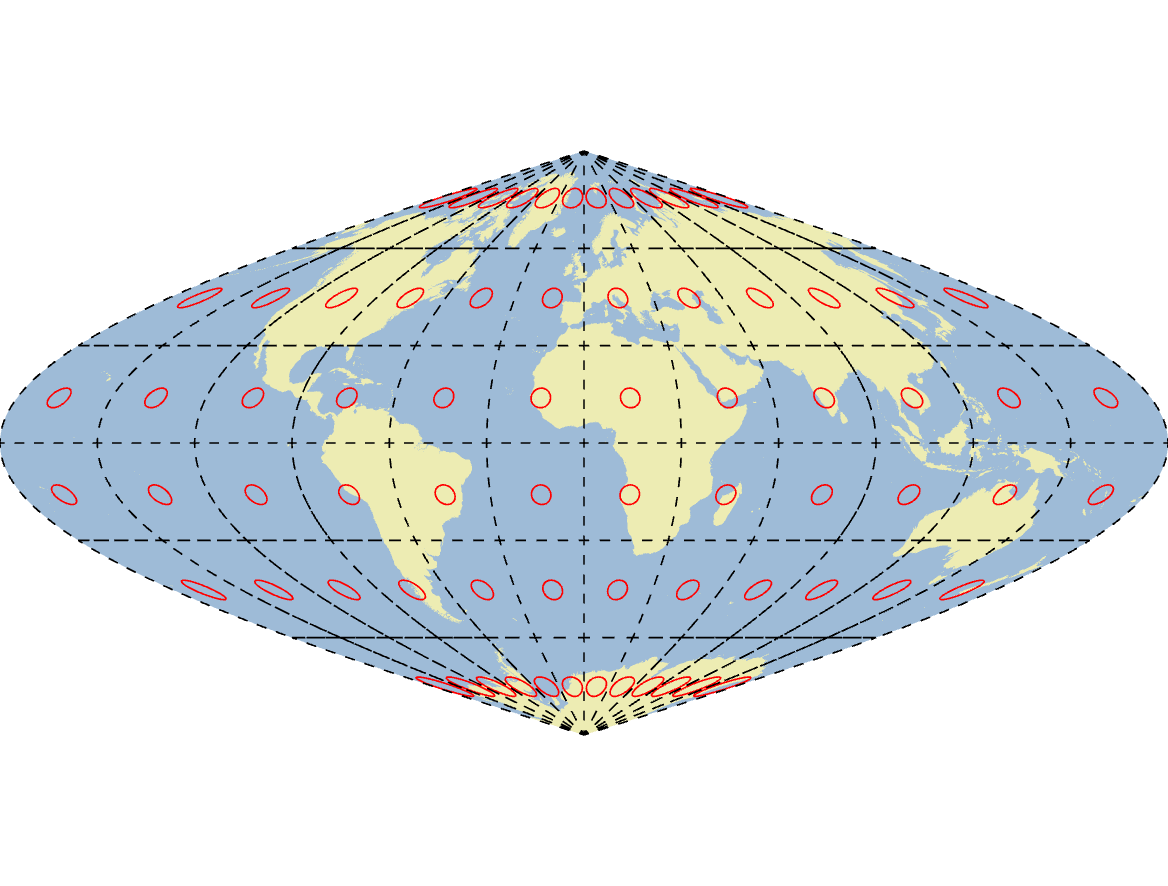
Classes of Projection
Conformal: Shapes are preserved.
Equal-area: Areas is preserved.
Equidistant: Distance is preserved (*limited)
True-direction: Direction is preserved (*limited)
Compromise: Splits the difference for aesthetics
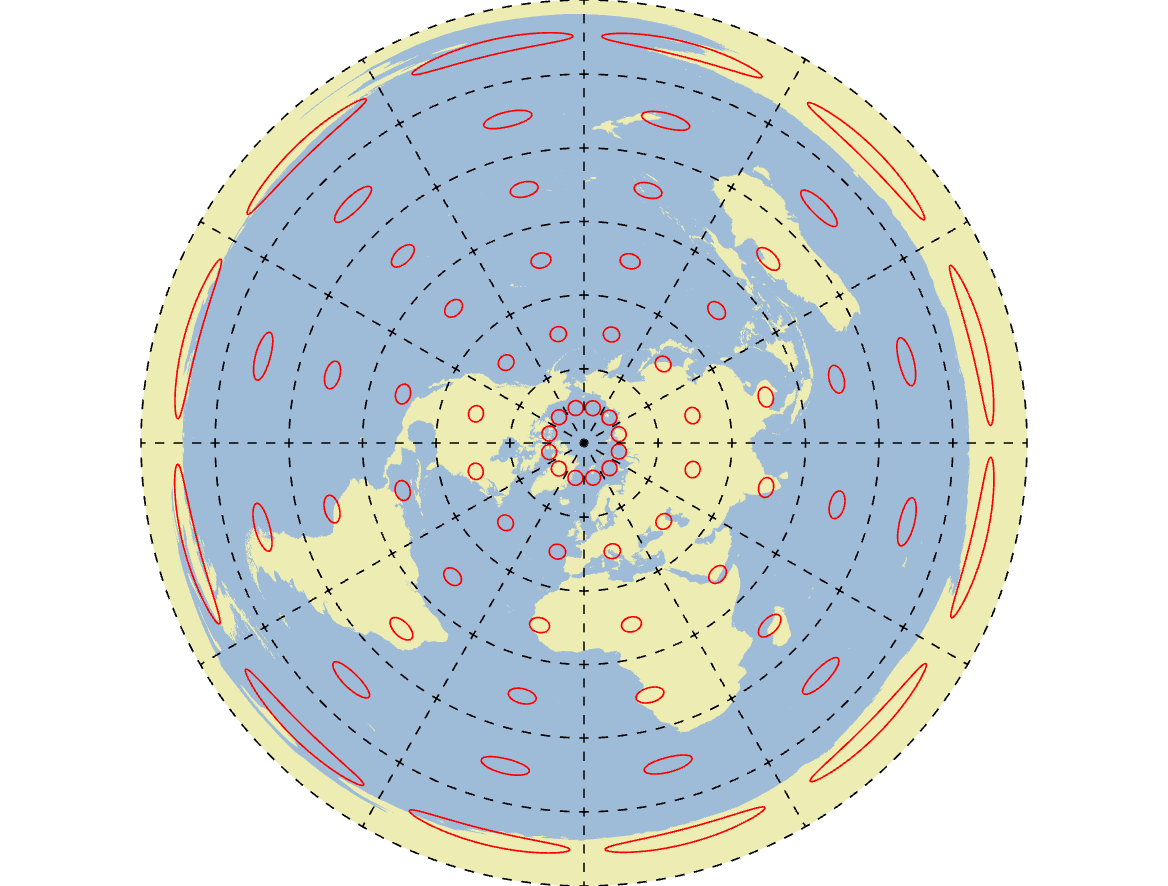
Conformal Projections
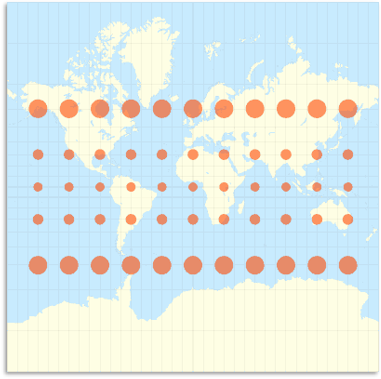
Conformal Projections
No angular deformation, but area is severely distorted.
Scale changes across the map, poor for measuring distances or areas.
Lambert Conformal Conic
Equal Area
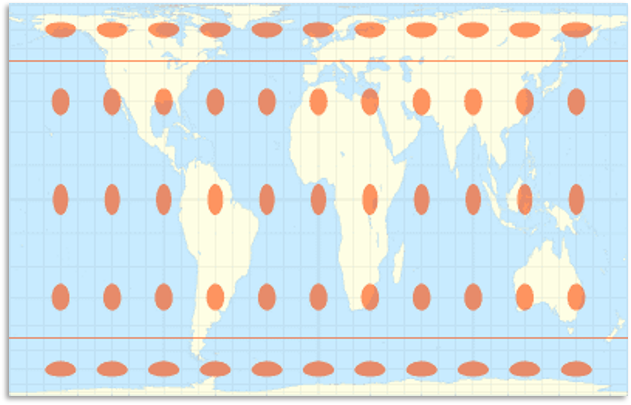
Equal Area
Preserves area but angles/shapes are deformed.
Very useful in GIS where area must be preserved for land analysis.

Albers Equal Area
Universal Transverse Mercator
Globe is divided into strips 6 degrees wide. Zones span from 80N to 80S.
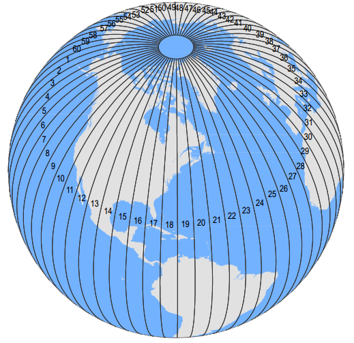
Universal Transverse Mercator
Each zone is projected on a transverse cylinder.
Universal Transverse Mercator (UTM)
Little distortion within zones – great for mapping small areas.
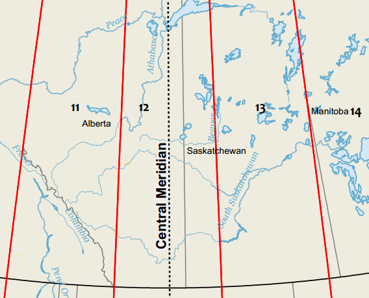
UTM Zone 8
Macknezie River Delta: a long, narrow feature
UTM Zone 10
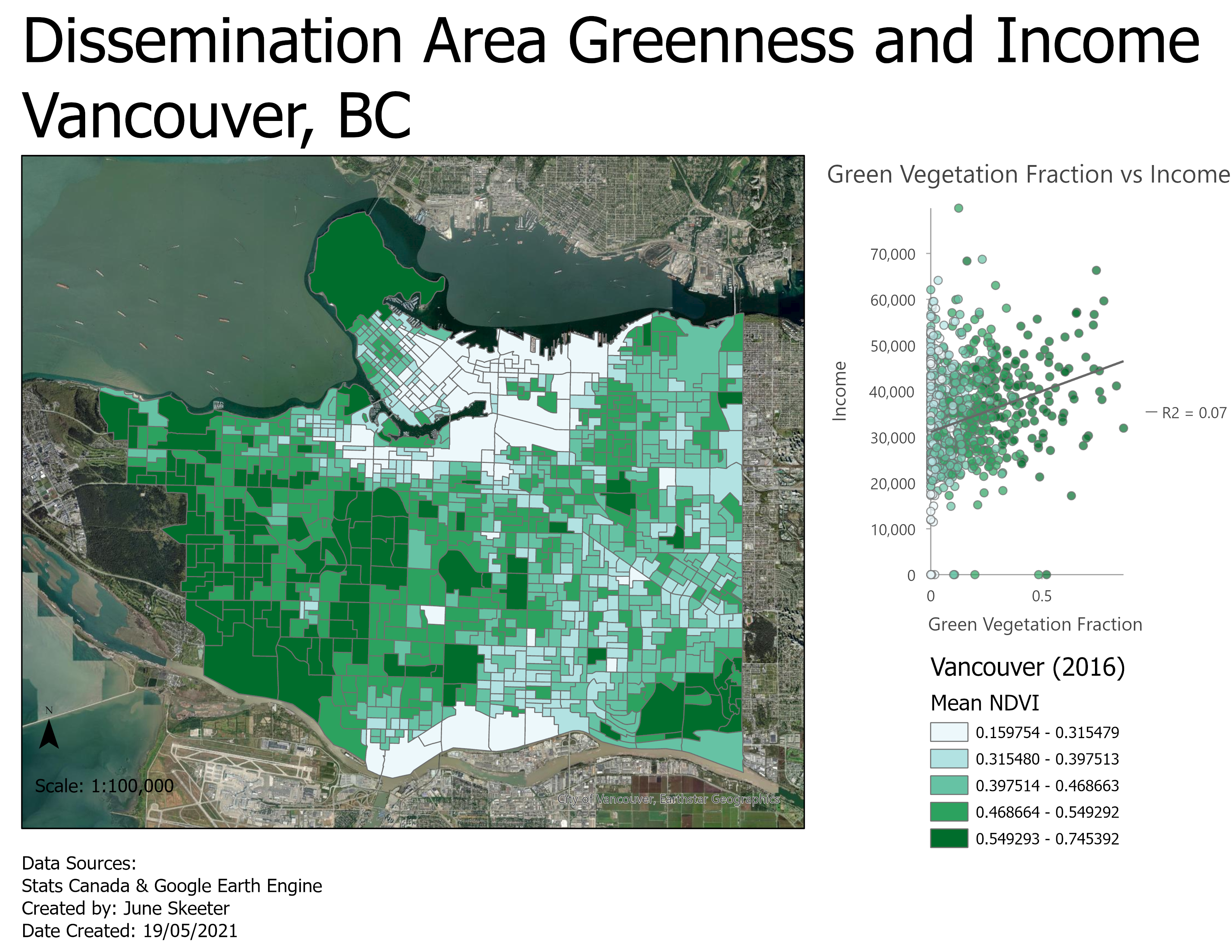
City of Vancouver: a small area
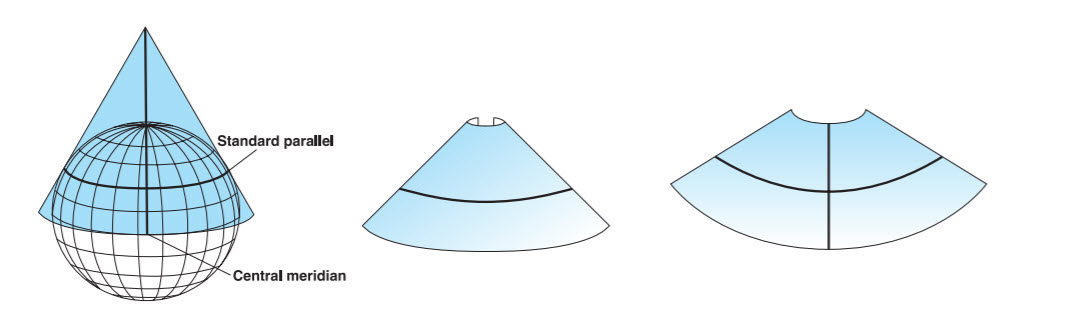
Tearing: All projections have tearing (edges)
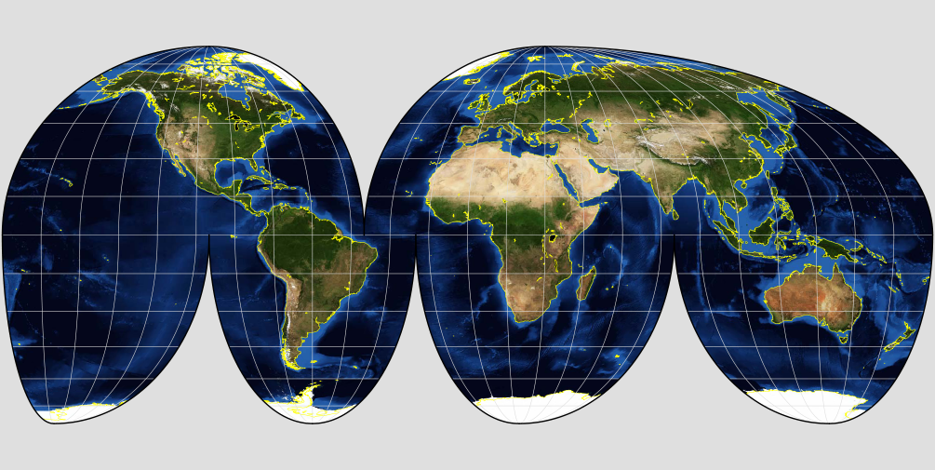
Shearing - Shapes/angles contorted
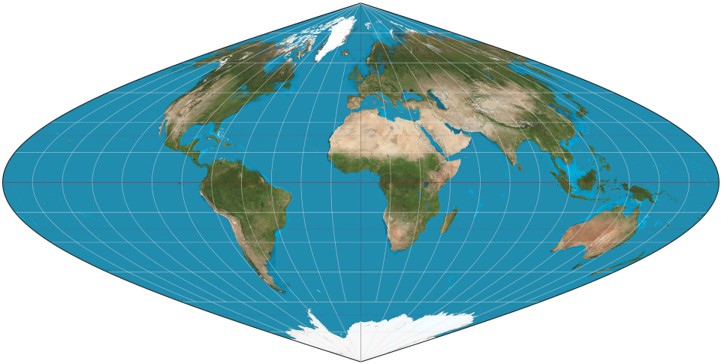
Compression: Changes to area
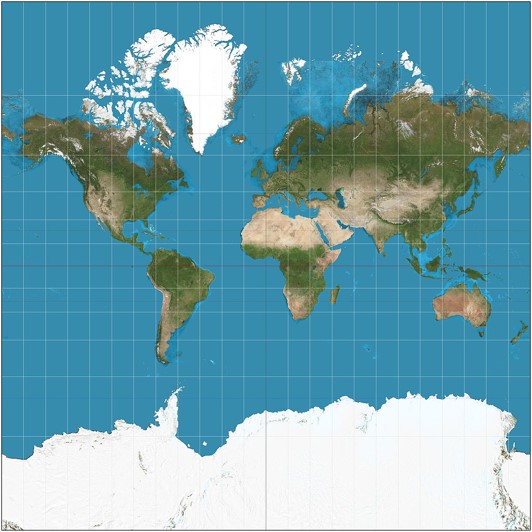
Compression: Changes to area
Compromise
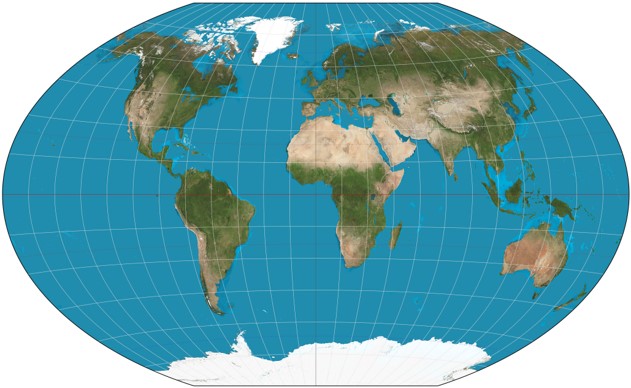
Strikes a balance between for aesthetics.
What projection is right for my map?
There isn't a "correct" answer here, but there are definitely wrong answers. You can typically get similar results with a handful of different projections, depending on your application.
Things to Think About
Where do the data come from?
- Some organizations use a standard projection
- Stats Canada: Lambert Conformal Conic
What is the map's purpose?
- Conformal/compromise are aesthetically pleasing.
- Navigational maps, use conformal, equidistant, etc.
- Thematic map (densities) use equal area.
Scale
The relationship between distance on a map to distance in the real world.
How much smaller than reality is the map?

Small Scale
Zoomed out, large area, more generalization, less detail.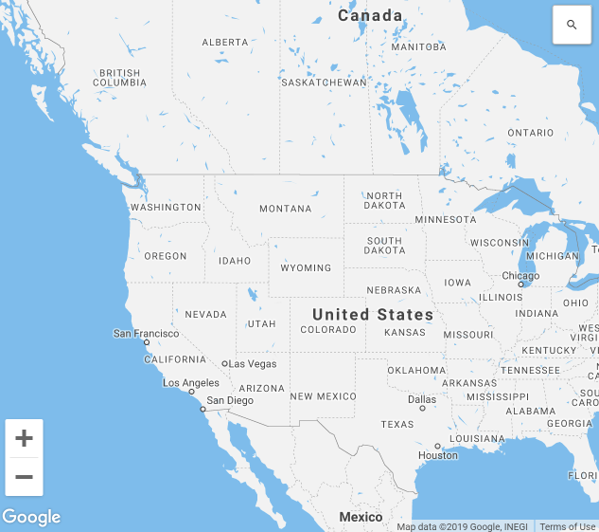
Large Scale
Zoomed in, small area, more detail, less generalization.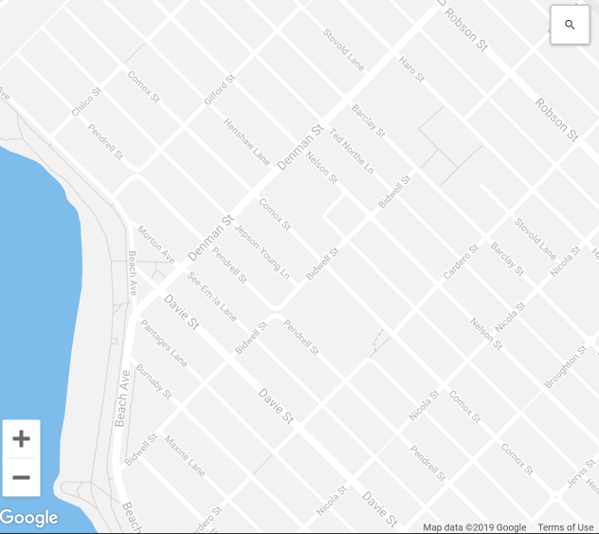
Small Scale 1:10,000,000
1/10,000,000 = 0.0000001

Large Scale 1:1,000
1/1,000 = 0.001

Scale
All maps require simplification of real world features, amount depends on map scale:
-Smaller scale maps require more generalization.
-Larger scale maps can include more detail.
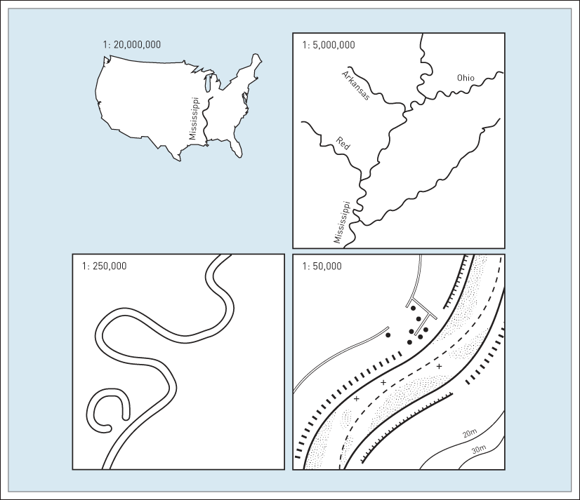
Scale & Projection
Map scale will impact our choice of projection.
Projections that work at 1:000 aren't necessarily suited for a 1:10,000,000 map.
Scale & Projection
With conformal projections like the Mercator, scale changes with position on the map.