Flattening the Blue Marble
This is what earth looks like when you take a picture of it from 29,000 kilometers away. This is the original Blue Marble photo, taken from Apollo 17.

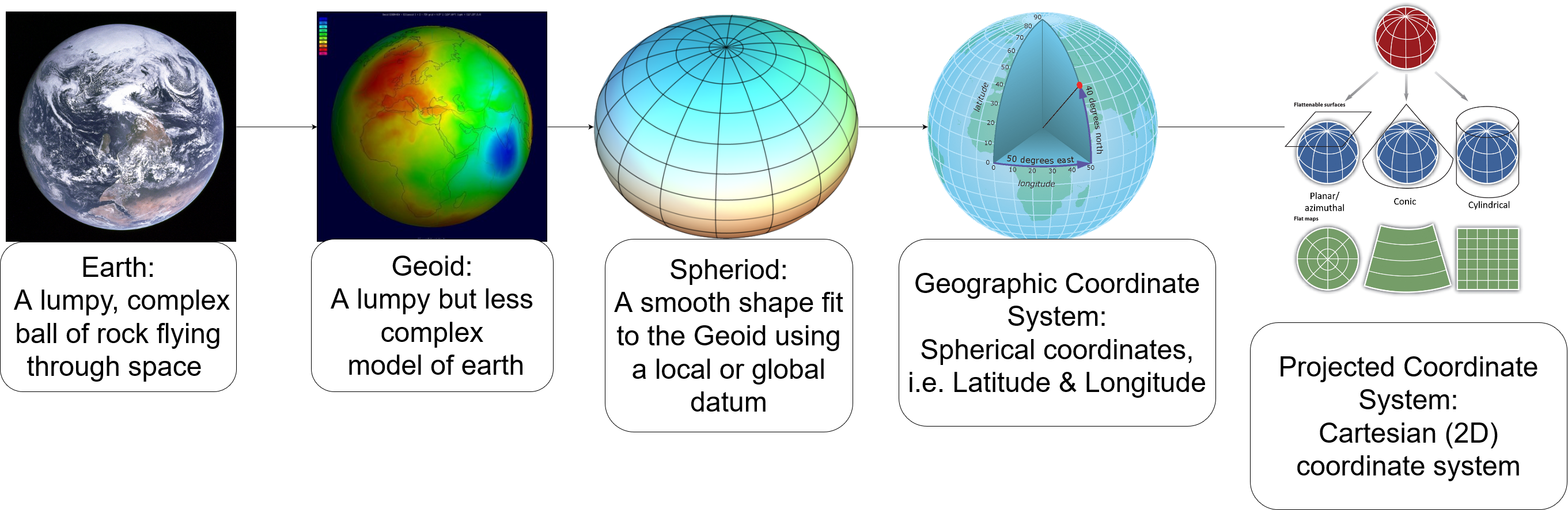
Earth
Multiple distortions from idealized sphere:
-Topography
-Gravity Differentials
-Centrifugal Force
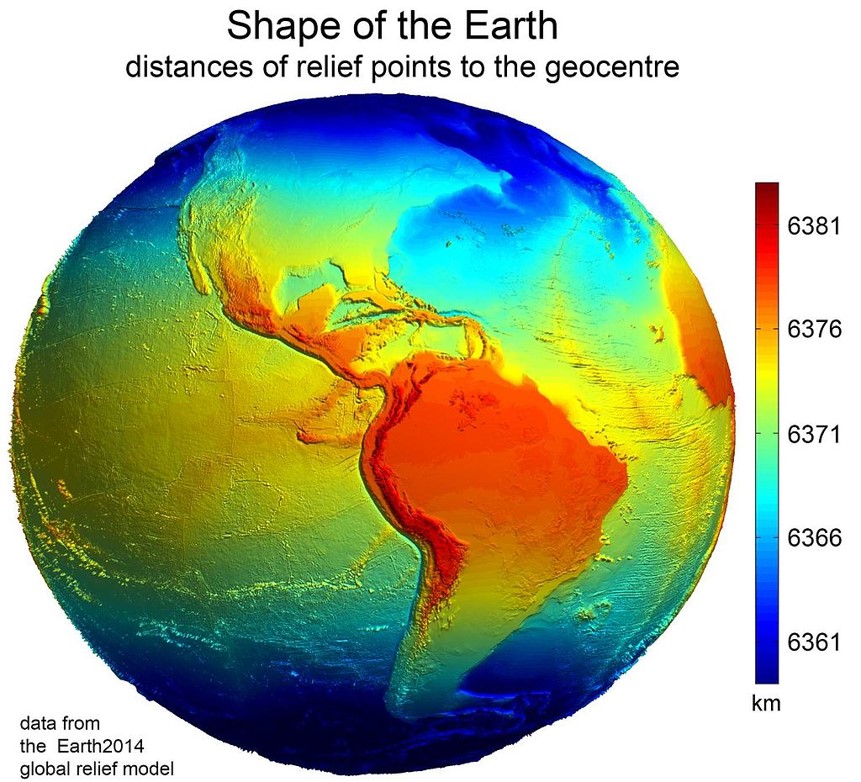
Ignore Topography!?
In most applications, topography isn't explicitly needed.
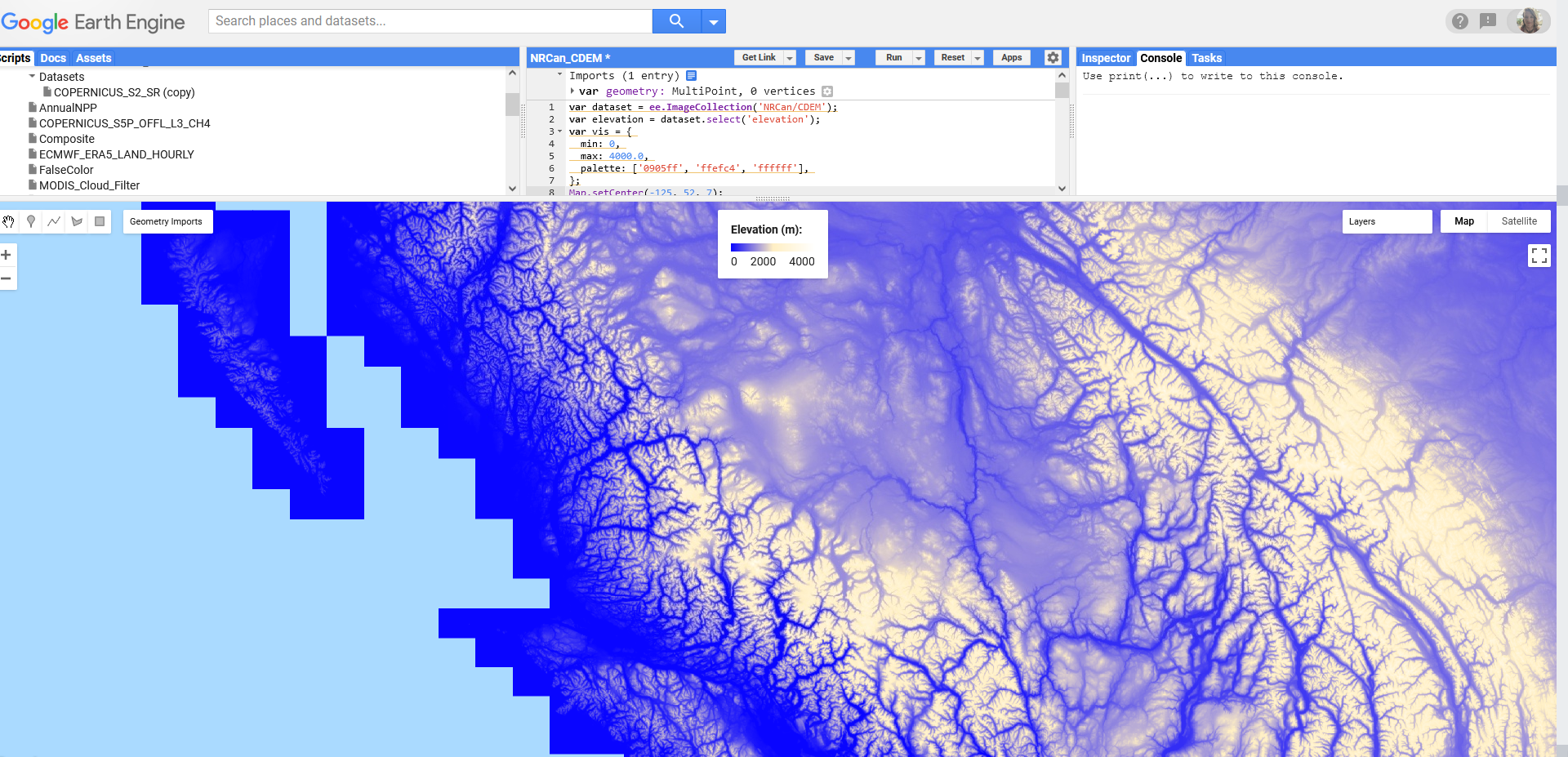
- We can account for it separately if necessary using digital elevation models or contour lines.
Digital Elevation Model
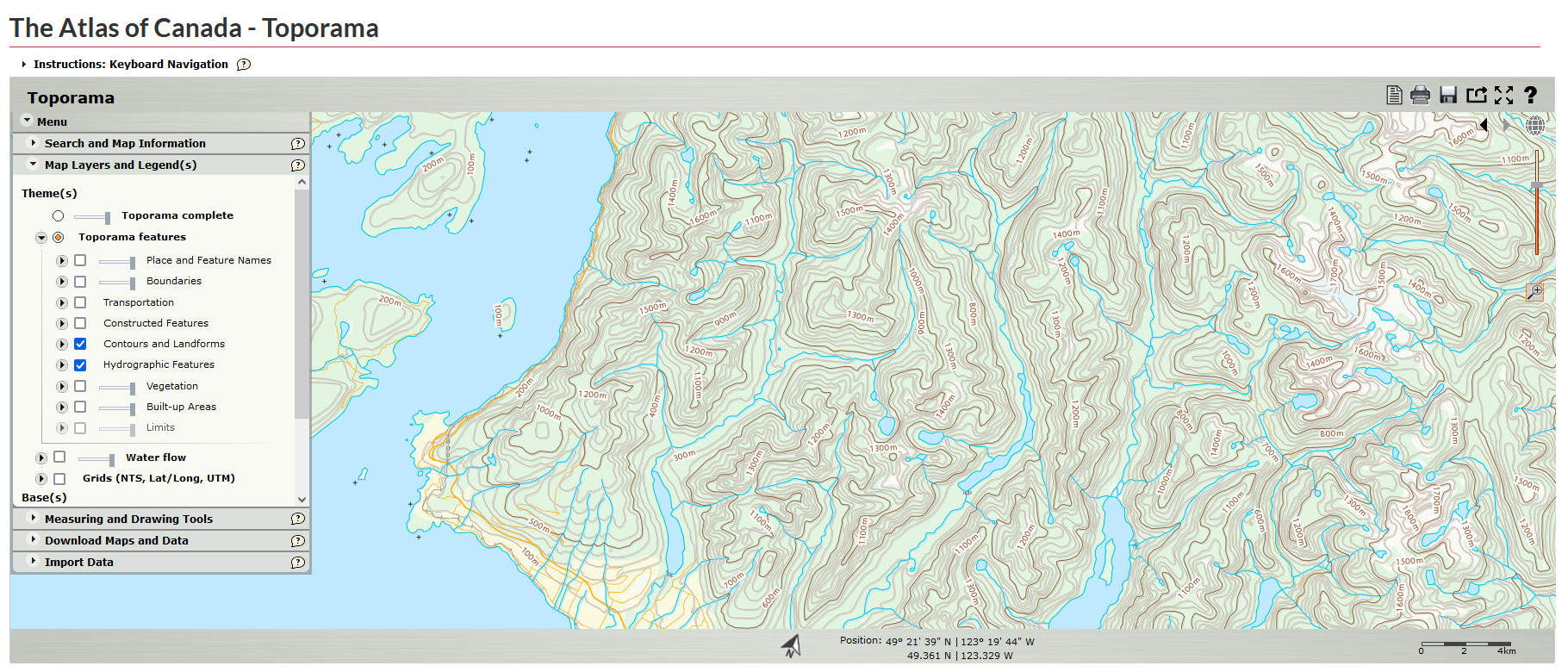
Contour Lines
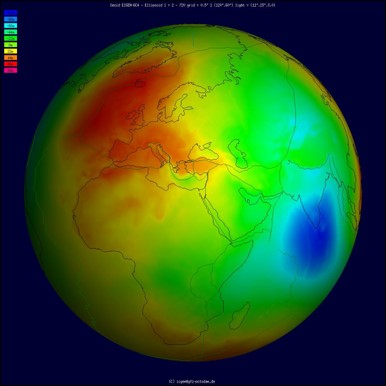
Geoid
Simplification of Earth:
-Smooths topography
-Gravity differences measured by satellites
-Differences in surface heights (180 m)
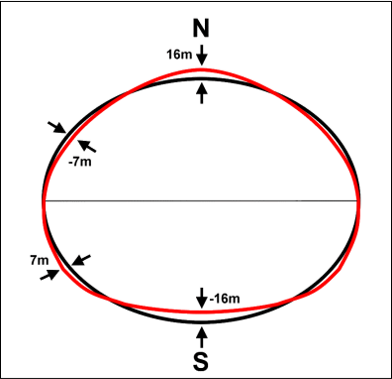
The Oblate Spheroid
A close approximation of Earth's shape
-Topography
-Gravity Differentials
-Centrifugal Force
A Datum
A system to link the oblate spheroid to the geoid
-Connect the coordinates to the earth’s surface
Local Datum
Fits geoid very well in a particular region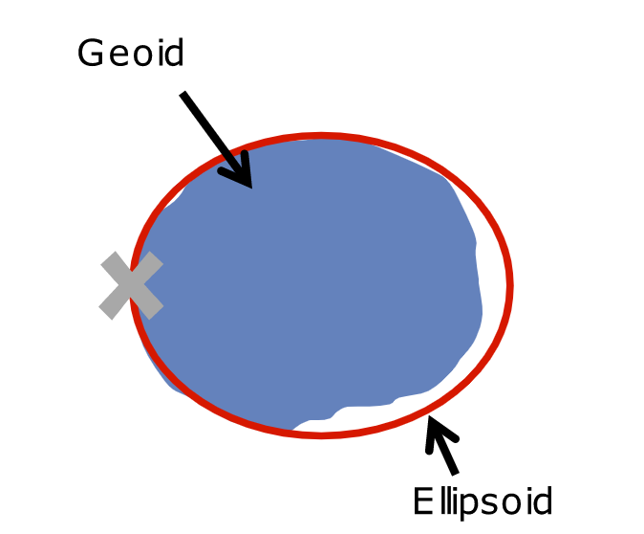
Global Datum
Fits the geoid fairly well everywhere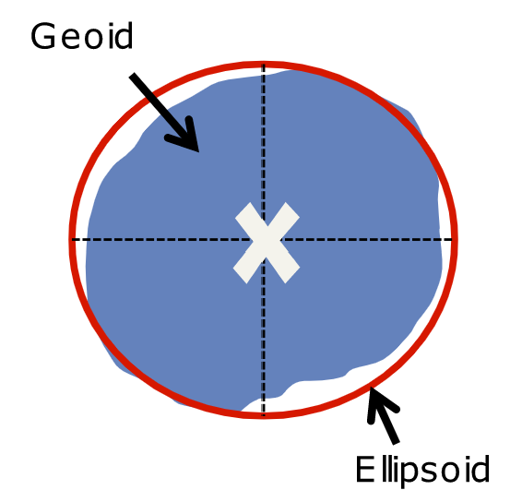
Local Datum
Fits geoid very well in a particular region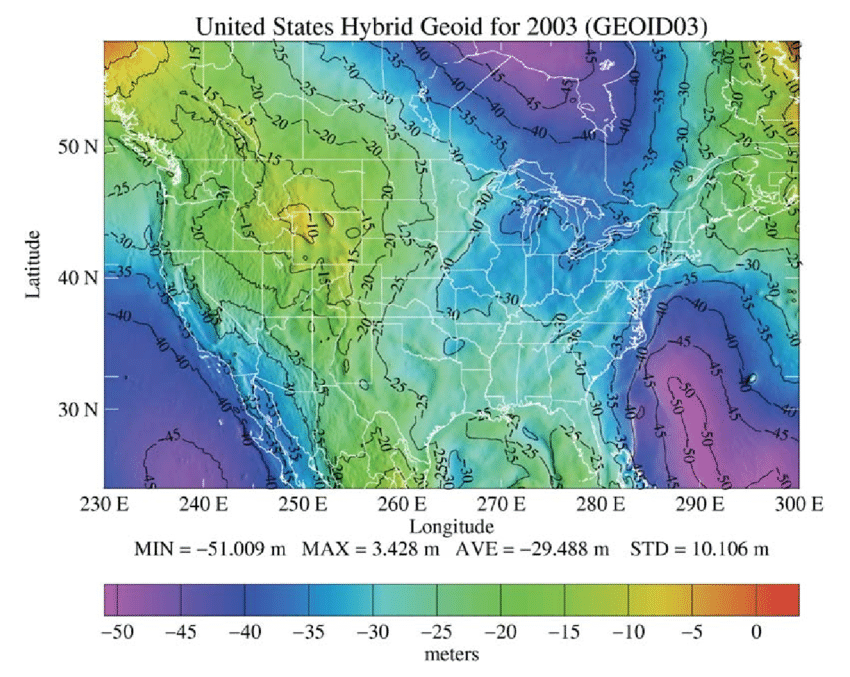
Global Datum
Fits the geoid fairly well everywhere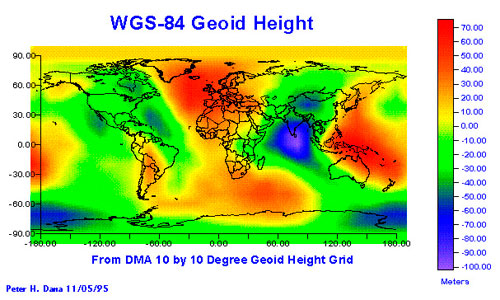
Only Minor Differences
For some cases, either datum is suitable.
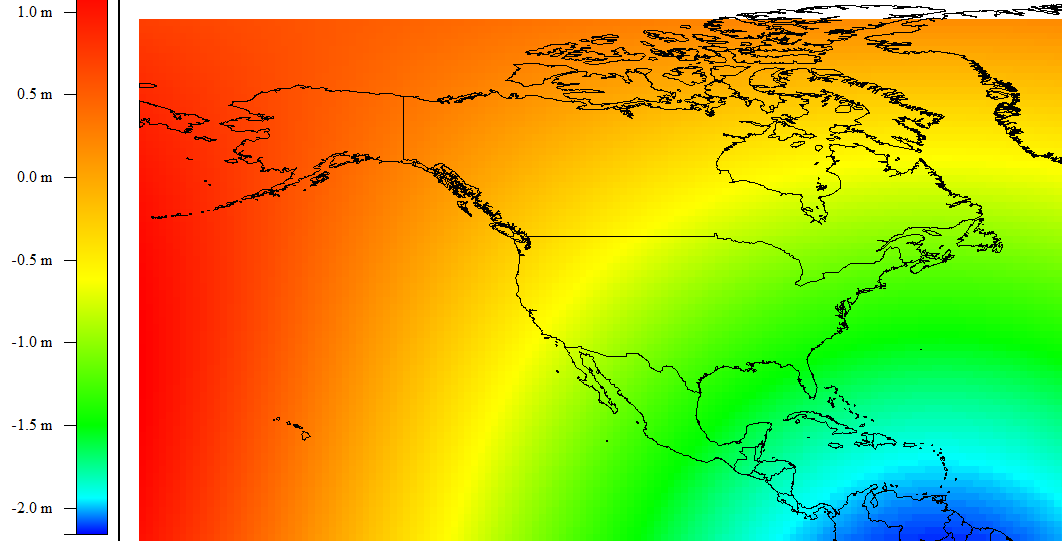
Only Minor Differences
A local datum is better for small areas like a city. For global maps, you always need a global datum.

Geographic Coordinate System (GCS)
Spherical Coordinate System for identifying locations on the spheroid.
-All GCS are tied to a specific datum.
Geographic Coordinate System (GCS)
Latitude/Longitude
- Fixed to the surface of spheroid
- Angular distance from equator and prime meridian
- Location on a 3D object with just 2 numbers

Latitude

Distance in degrees form Equator: -90°(South) to +90°(North)
Longitude

Distance in degrees Prime Meridian: -180° (West); to +180° (East)
Latitude/Longitude
Decimal Degrees
- Vancouver BC: 49.261111, -123.113889
- Sydney NSW: -33.865, 151.209444
Degrees Minutes Seconds
- Vancouver BC: 49°15′40″N 123°06′50″W
- Sydney NSW: 33°51′54″S 151°12′34″E
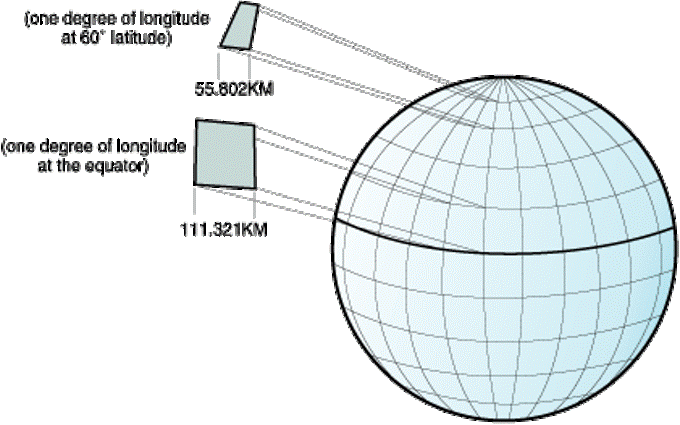
An Important Caveat!
Meridians converge!
- Distance between degrees of longitude decreases with increasing latitude
Making a Flat Map
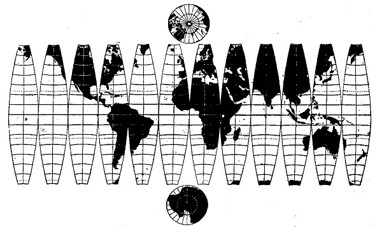
Making a Flat Map
Displaying Lat/Lon in 2D doesn't work well
- Causes things to look "scrunched"
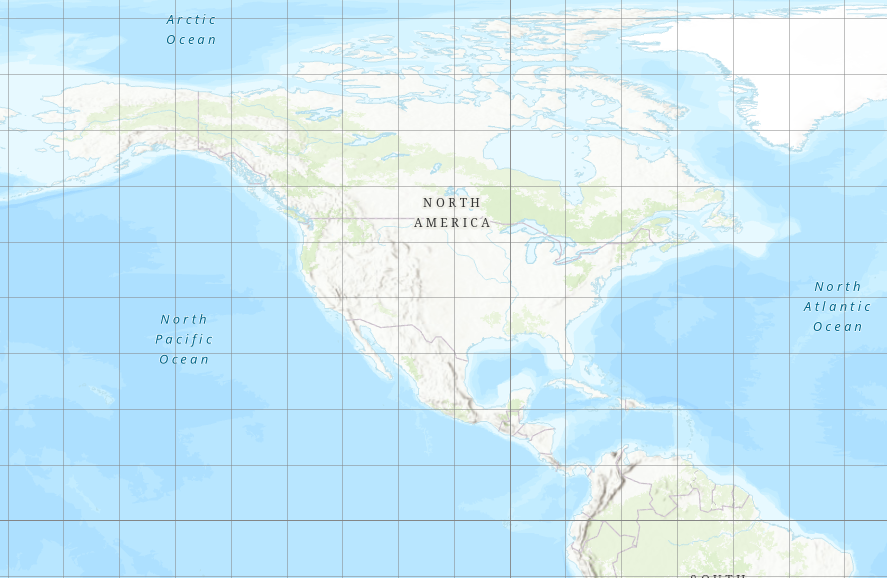
Making a Flat Map
We have to apply a projection
- Converts to linear units
- Allows distance/area calculations
- Makes things look better
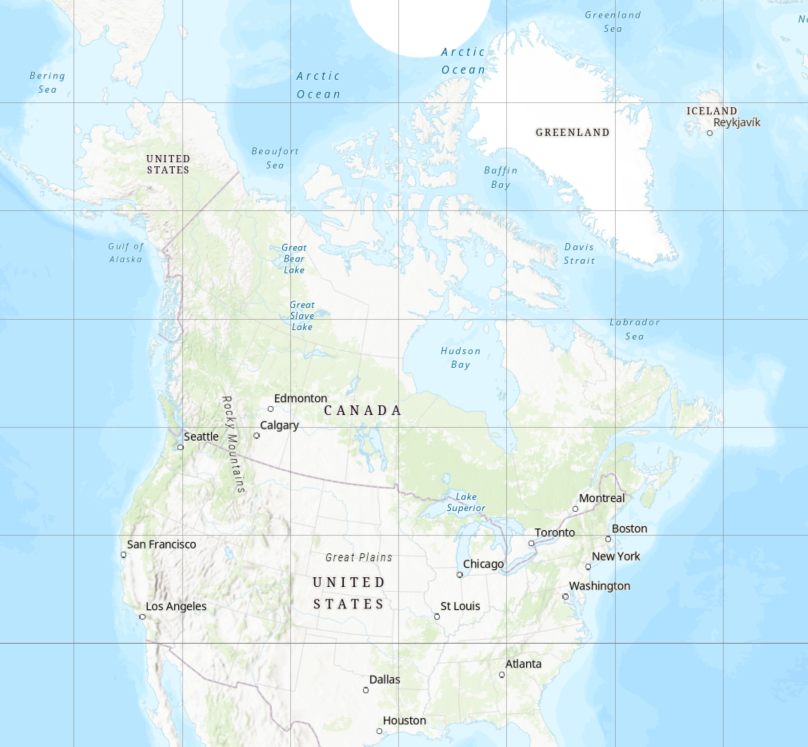
Projected Coordinate Systems
A map projection is a flattened GCS. Imagine sending rays of light through the ellipsoid onto a flat surface, the resulting image is a projection.
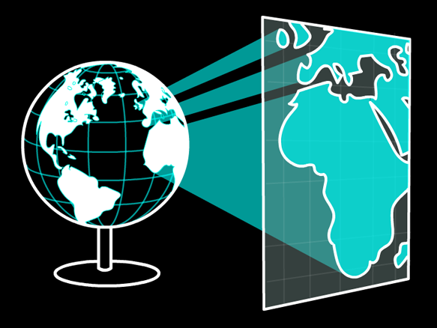
Steps of Abstraction